优化算法入门系列文章目录(更新中):
1. 模拟退火算法
2. 遗传算法
一. 爬山算法 ( Hill Climbing )
介绍模拟退火前,先介绍爬山算法。爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如图1所示:假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。
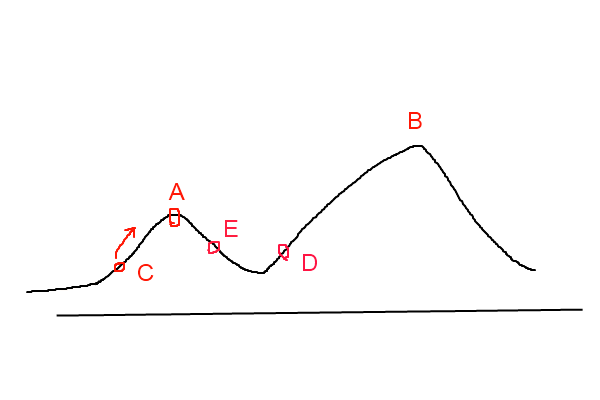
图1
二. 模拟退火(SA,Simulated Annealing)思想
爬山法是完完全全的贪心法,每次都鼠目寸光的选择一个当前最优解,因此只能搜索到局部的最优值。模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。以图1为例,模拟退火算法在搜索到局部最优解A后,会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点,于是就跳出了局部最大值A。
模拟退火算法描述:
若J( Y(i+1) )>= J( Y(i) ) (即移动后得到更优解),则总是接受该移动
若J( Y(i+1) )< J( Y(i) ) (即移动后的解比当前解要差),则以一定的概率接受移动,而且这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定)
这里的“一定的概率”的计算参考了金属冶炼的退火过程,这也是模拟退火算法名称的由来。
根据热力学的原理,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:
P(dE) = exp( dE/(kT) )
其中k是一个常数,exp表示自然指数,且dE<0。这条公式说白了就是:温度越高,出现一次能量差为dE的降温的概率就越大;温度越低,则出现降温的概率就越小。又由于dE总是小于0(否则就不叫退火了),因此dE/kT < 0 ,所以P(dE)的函数取值范围是(0,1) 。
随着温度T的降低,P(dE)会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程,我们以概率P(dE)来接受这样的移动。
关于爬山算法与模拟退火,有一个有趣的比喻:
爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
下面给出模拟退火的伪代码表示。
三. 模拟退火算法伪代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
代码
/*
* J(y):在状态y时的评价函数值
* Y(i):表示当前状态
* Y(i+1):表示新的状态
* r: 用于控制降温的快慢
* T: 系统的温度,系统初始应该要处于一个高温的状态
* T_min :温度的下限,若温度T达到T_min,则停止搜索
*/
while( T > T_min )
{
dE = J( Y(i+1) ) – J( Y(i) ) ;
if ( dE >=0 ) //表达移动后得到更优解,则总是接受移动
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
else
{
// 函数exp( dE/T )的取值范围是(0,1) ,dE/T越大,则exp( dE/T )也
if ( exp( dE/T ) > random( 0 , 1 ) )
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
}
T = r * T ; //降温退火 ,0<r
/*
* 若r过大,则搜索到全局最优解的可能会较高,但搜索的过程也就较长。若r过小,则搜索的过程会很快,但最终可能会达到一个局部最优值
*/
i ++ ;
}
|
四. 使用模拟退火算法解决旅行商问题
旅行商问题 ( TSP , Traveling Salesman Problem ) :有N个城市,要求从其中某个问题出发,唯一遍历所有城市,再回到出发的城市,求最短的路线。
旅行商问题属于所谓的NP完全问题,精确的解决TSP只能通过穷举所有的路径组合,其时间复杂度是O(N!) 。
使用模拟退火算法可以比较快的求出TSP的一条近似最优路径。(使用遗传算法也是可以的,我将在下一篇文章中介绍)模拟退火解决TSP的思路:
1. 产生一条新的遍历路径P(i+1),计算路径P(i+1)的长度L( P(i+1) )
2. 若L(P(i+1)) < L(P(i)),则接受P(i+1)为新的路径,否则以模拟退火的那个概率接受P(i+1) ,然后降温
3. 重复步骤1,2直到满足退出条件
产生新的遍历路径的方法有很多,下面列举其中3种:
1. 随机选择2个节点,交换路径中的这2个节点的顺序。
2. 随机选择2个节点,将路径中这2个节点间的节点顺序逆转。
3. 随机选择3个节点m,n,k,然后将节点m与n间的节点移位到节点k后面。
五. 算法评价
模拟退火算法是一种随机算法,并不一定能找到全局的最优解,可以比较快的找到问题的近似最优解。 如果参数设置得当,模拟退火算法搜索效率比穷举法要高。
 Linuxeden开源社区
Linuxeden开源社区